[음향] Sample Rate(샘플 레이트), Bit Depth(비트뎁스)
오늘은 Sample Rate 와 Bit Depth 에 대해서 포스팅하겠습니다.
이 둘을 설명하시 전에 아날로그에서 디지털(ADC) 변화과정을 알아야 합니다.
시간을 예시로 들어보자면
0ㅊ초에서 1초 사이에는 0.1초, 0.02초 0.000004초.. 같이
사실 상 무한한 시간이 있습니다.
아날로그 상에서는 어떠한 두 공간이나 시간 사이를 따지고보면 무한하게
쪼갤 수 있다는 것이 아날로그 신호입니다.
즉 다시 말하면 아날로그는 양 또는 데이터를 연속적으로 변환하는 물리량으로 표현 하는 것입니다.
반면에 디지털 신호는, 연산처리 상 무한대라는 개념이 존재할 수 없기 때문에
인간이 인지할 수 없을 정도거나 상황적으로 보았을 때 그렇게 큰 오차를 내지
않는 한도 내에서 유한적으로 조갤수 있습니다.
즉 다시 말하면 디지털은 양 또는 데이터를 2진수로 표현하는 것을 말합니다.
두개를 요약하면 아날로그는 연속적이며 빈 공간이 없고, 디지털은 신호는 불연속적이며 빈공간 있다는 차이점이다.

아날로그 신호를 디지털 데이터로 저장하기 위해서 필요한 과정이 Sampling 입니다.

특정 시간 간격으로 아날로그 진폭을 캡쳐하여 만들어진 Sample(화살표)들에 대한 각자의
Sine함수(점선)를 더 하고 사이에 생기는 빈 공간의 값을 유추하여 곡선 형태로 만들어 내는데
이를 Interpolation 이라고 부른다.
Sample Rate
아날로그 신호의 진폭 값을 특정 시간마다 캡쳐하여 생긴
Sample 들이 이어져서 디지털 신호로 만드는 표본화 과정을 말합니다.
(표본화 : 일정한 시간 간격으로 아날로그 신호의 레발값을 취득하는 단계)
간단하게 설명하면 Sample Rate는 1초당의 샘플의 개수를 의미합니다.
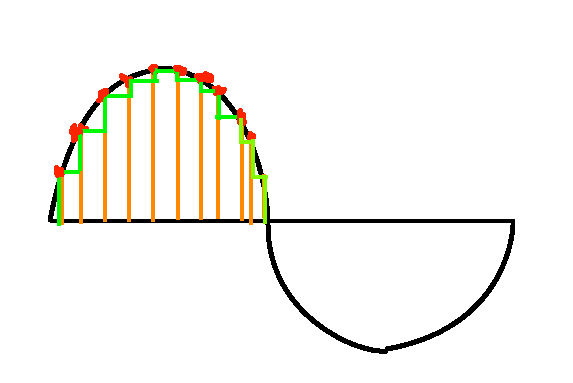
단위는 Hz를 사용하며 보통 CD에서는 44.1kHz의 Sample Rate를 사용합니다.
우리가 여기서 2가지 이론으 존재합니다.
사람이 들을수 있는 Audio Frequency(20Hz ~20kHz) 들을수 있는 범위입니다.
샤논 이론과 나이키스트 이론이 있으며 간단하게 요약을하면
샤논 이론은 2배 이상의 샘플링해야 원신호를 복원할수 있다.
나이키스트 이론은 원신호 최대 주파수 2배를 샘플링해야 원신호를 복원 할수 있다.
샤논이론은 즉
우리가 듣는 소리 100Hz들을 듣고 싶으면 200Hz를 해야 들을수 있다는 이론이고
나이키스트 이론은 20Hz ~ 20kHz 범위에서 최대 주파수 즉 40kHz를 샘플링 하는것이라고 생각하면 편안합니다.
특정 신호가 가진 최대의 진동수 보다 2배 이하로 Sampling을 하였을때 기존에 없던
신호인 생기는 현상이 발생할수 있습니다.(Aliasing)

Sample Rate의 1/2에 해당하는 주파수를 Nyquist Frequeny 라고 하는데, 다르게 말하면
Sampling을 할 때 Nyquist Frequeny를 넘는 소리는 Aliasing 이 생긴다고 말할 수 있습니다.
Nyquist Frequeny를 중심으로 Aliasing이 좌우대칭형으로 생성 이 되기 때문에 Aliasing을
Fold Over라고도 합니다.

Nyquist Frequency를 넘긴 주파수가 몇 Hz에서 Aliasing 되는지는 이 식을 통하여 알 수 있습니다.
Aliasing 을 발생을 차단하기 위해서 두가지 방법이있습니다.
Anti -Aliasing, Over Sampling있습니다.
Anti Aliasing은
공기중에는 Radio Frequency나 동물 소리 같이 Audio Frequency 이상의 소리도
사람이 듣지 못할 뿐 존재하는데, 이 경우 Nyquist Frequency를 초과하는 주파수에 Aliasing 이 생겨 날수 있다.
ADC로 들어가기 전에 Audio Frequency를 초과하는 소리를 Low Pass Filter를 거치게 되는데
이를 Anti Aliasing Filter라고 부른다.
하지만 Anti Aliasing Filter 같은 경우는 고음역대를 Cut하기 때문에 원소리에 소리를 왜곡 시킬수있다.
그래서 다음에 다온 방법이 Over Sampling 방식입니다.
Over Sampling은
원래 샘플링 주파수 주파수보다 4배 이상 높은 주파수로 샘플링 후
디지털 필터를 통해 원래 주파수를 만드는것을 말합니다.
Over Sampling 에서 중심적으로 보아야 할 것은
'아날로그 필터인 Anti Aliasing Filter 의 기울기를 완만하게 하면서 Aliasing 없는 음원을 구현하는 방법'

Bit Depth
진폭의 세밀함을 결정하는 값으로 높을수록 다이나믹 레인지가
커져 볼륨의 변화를 좀더 세밀하게 표현합니다.

44.1kHz 16Bit 라는 말은 곧 1초에 65536개의 선택 가능한 크기에 44100번 기록한다는 말입니다.
16Bit 2 16승으로 65536 dB로는 16 x 6 = 96dB 다이나믹 레인지를 갖습니다.
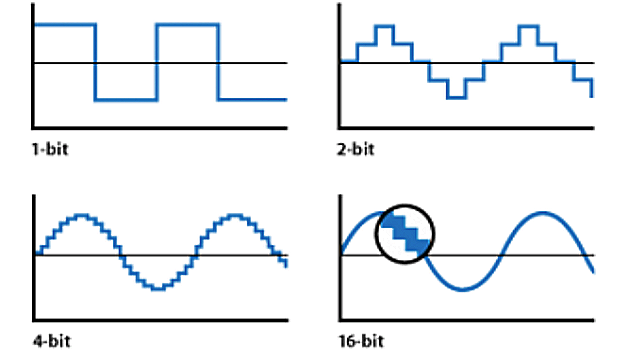
Bit가 올라갈수록 진폭 수가 많아져서 파형이 완만 한 형태를 이루게 됩니다.
하지만 확대해보면 역시 Square wav와 같은 모양을 하고 있고 아날로그 신호는
연속된 값이므로 정확한 기록은 불가능합니다.
그래서 신호가 입력되면 아래 그림과 같이 Bit에 다라서 근사값으로 인식해서 기록합니다(양자화 과정)
(양자화 : 표본화에서 없는 아날로그 기록을 근사값으로 반올리하는것)

우리가 ADC 과정에서
표본화(Sampling) - 양자화(Quantization) - 부호화(Coding) 순서입니다.
양자화 같은경우는 실제 아날로그 신호가 아닌 표본화를 통한 근사값이기 때문에
여기서 문제가 하나 발생할수 있습니다. 그것은 Quantiztion Error(양자화 에러가) 일어날수 있다.
양자화 에러는 실제 아날로그 값이 아닌 근사값으로 표기하기 때문에
실제 아날로그 값이 양자화 단계에서 떨어질때 발생합니다.
표본화 수치를 반올림하여 수치화 하기때문에 디지털 오디오에서 잡음이 발상할수 있다.
이 경우 해결 방법으로는 Bit를 높이면 정확도가 향상되므로 에러의 발생은 줄어들고
낮은 비트의 양자화 또는 높은 비트라도 레벨이 작은 경우 양자화 에러가 발생할수 있다.
또한 샘플링 시간이 길수록 에러 기간이 길어지게 되며 그 기간이 길어지게 되면 원신호와 다르다는 걸 인지하게 됩니다.
에러양은 샘플 양에 다라 차이가 없을 수 있지만 에러의 시간이 기냐 짧냐의 기준이 양자화 에러에 좀더 중요한 포인트입니다.